La loi de Poisson est une variable aléatoire entière à un paramètre (noté ). On note: 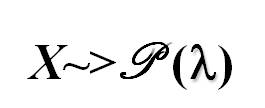
Sa distribution de probabilité est la suivante : pour k = 0, 1, 2, 3,
4,......
Son Espérance et sa Variance valent : λ .
Le paramètre d'une loi de Poisson apparaît donc concrètement comme la valeur moyenne prise par cette loi.
La loi de Poisson peut être définie comme régissant le nombre d'apparitions d'un phénomène quand deux conditions sont remplies :
(1) La probabilité d'apparition du phénomène sur un court intervalle de temps est proportionnelle à la durée de cet intervalle.
(2) La probabilité d'une apparition multiple du phénomène sur un très court intervalle de temps est négligeable (infiniment petit du second ordre).
Compte tenu de ces conditions, on qualifie parfois la Loi de Poisson de "loi des événements rares".
La loi de Poisson est, par exemple, celle qui régit les arrivées dans les files d'attente ou les passages de véhicules sur les routes.
Il existe des tables de la loi de Poisson : ces tables sont de deux types, les premières fournissent pour une valeur du paramètre et pour une valeur k la probabilité ponctuelle P( X = k ); les secondes fournissent les probabilités cumulées P( X k )
Remarques :
1) La somme de deux lois de Poisson indépendantes est une loi de Poisson.
Son paramètre est égal à la somme des paramètres des deux lois de départ.
2) On peut approcher une loi binômiale de paramètres n et p par une loi de Poisson de paramètre n p dès que n est suffisamment grand (on prendra n > 50) et que np est suffisamment petit (on prendra np < 15))