LA LOI NORMALE
La Loi Normale est une variable continue (on l'appelle aussi loi de Gauss, loi de Laplace-Gauss, 2ème Loi de Gauss).
Une Loi normale possède deux
paramètres : le premier correspond à son espérance (sa "moyenne") et
sera donc noté : m; le second correspond à son écart-type (à la racine carrée
de sa Variance) et sera donc noté .
Une loi normale de paramètres m
et sera notée : N (m,σ).
Comme c'est une variable aléatoire continue, les probabilités ponctuelles sont nulles et l'on définit une densité de probabilité :
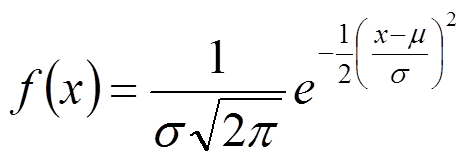
Ne vous affolez pas, cette formule est compliquée mais n'est d'aucune utilité pratique.
Quand on aura à manipuler une loi normale, on utilisera la propriété suivante :
, on aura T→N(0,1)
Compte tenu de cette propriété, seule reste à étudier la loi normale centrée réduite.
N(0,1) :
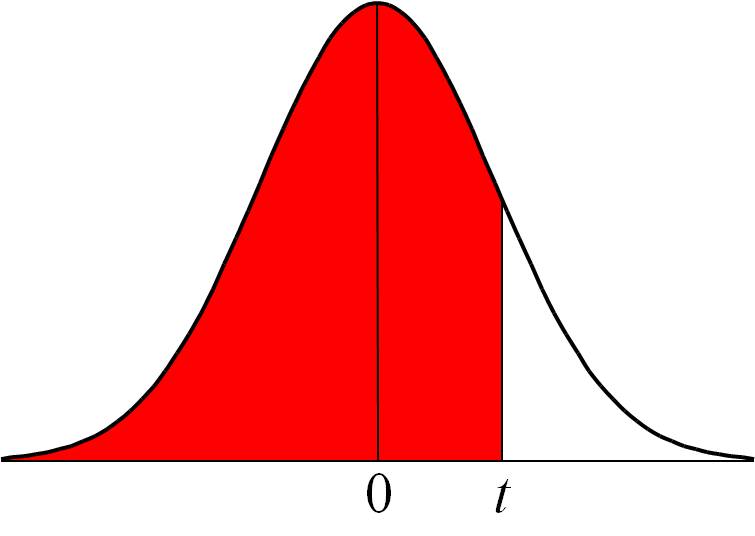
On sait que la surface sous cette courbe représente la probabilité, donc on peut définir la fonction de répartition (probabilité d'être avant une valeur donnée) comme étant la surface sous la courbe de - à la valeur considérée (cf. Table 3). On note cette fonction de répartition : .
Ainsi :
En effet, la probabilité d'être après b est égale à 1 moins la probabilité d'être avant et la probabilité d'être entre a et b est égale à la probabilité d'être avant b moins la probabilité d'être avant a.
Notez que l'on a utilisé des inégalités "larges" ( et ) mais que l'on aurait pu sans problème utiliser des inégalités strictes (< et >) puisqu'en rajoutant une valeur ponctuelle, on ne change pas la probabilité dans le cas d'une variable continue.
On a donc ramené tout calcul de probabilité sur une loi normale à un calcul de fonction de répartition de N(0,1).
Une Table nous donne pour toute valeur de t positive la valeur de (t) : les deux premières décimales de t se trouvent sur la première colonne et la troisième décimale sur la première ligne.
Par exemple : Π(1,12) = 0,8686 (ligne 1,1 et colonne 0,02)
Π(0,37) = 0,6443 (ligne 0,3 et colonne 0,07)
Π(-1,12) = 1-0,8686 = 0,1314
Combinaison de lois normales :
Toute combinaison linéaire de lois normales indépendantes est une loi normale; les paramètres se déterminent par manipulation d'espérances et de variances.
En effet, le premier paramètre d'une loi normale, c'est l'espérance. Or l'espérance de la somme est égale à la somme des espérances (cf. Variables aléatoires, Manipulation des opérateurs).
Le second paramètre, c'est l'écart-type, la racine carrée de la variance. Or la variance de la somme se ramène pour des variables indépendantes à la somme des variances (la covariance étant nulle) (cf. idem qu'au-dessus)
Remarque : On aurait, par exemple, dans les mêmes conditions :
Approximations
1) Poisson par Normale :
On peut approcher une loi de Poisson par une loi Normale dès que est suffisamment grand (on prendra > 15) :
2) Binômiale par Normale :
On peut approcher une loi binômiale par une loi Normale dès que n est suffisamment grand et p suffisamment proche de 0,5 (on prendra n > 100 et npq > 5)
Remarque très importante :
Dans les approximations, on approche une variable aléatoire discrète ou entière (binômiale ou Poisson) par une variable continue (la loi normale).
Si on se sert de ces approximations pour calculer des probabilités ponctuelles, on obtiendra 0 puisque les probabilités ponctuelles d'une variable continue sont nulles.
Il faut donc
remplacer la valeur ponctuelle k
par un intervalle
centré sur k égal à [ k-½ , k+½ ]
(Cette opération s'appelle une correction de continuité)