Savez-vous compter ?

Prenons les 5 lettres :

Combien y a-t-il de façons différentes de choisir 3 lettres parmi ces 5 ?

Posée ainsi, la question est ambiguë, on ne peut pas y répondre, sauf par d'autres questions :

La première qui vient à l'esprit est : "est-ce qu'on a le droit de prendre plusieurs fois la même ?", c'est à dire AAA ou ABA sont-ils des choix autorisés ?

Cette notion est évidemment fondamentale, c'est la notion de répétition; reformulée, la question devient : "la répétition est-elle possible ?"

Eh bien, ça dépend, on peut autoriser la répétition ou non, ça nous fait donc deux problèmes à résoudre : avec et sans répétition.

Une remarque : autoriser la répétition revient à dire qu'on peut choisir plusieurs fois la même lettre, donc à dire qu'on la remet dans le "sac" après l'avoir tirée; la notion de choix avec répétition est donc très proche de la notion de tirage avec remise.

La seconde question qui doit vous venir à l'esprit est : "Est-ce que ABC et CBA c'est pareil ?", autrement dit, en meilleur français : "Deux choix qui ne diffèrent que par l'ordre des lettres choisies sont-ils comptés comme 1 seul et même choix ou non ?"

On voit apparaître là la seconde notion fondamentale : l'ordre.

Là aussi, ça dépend, on peut décider que l'ordre ne compte pas (donc dire que ABC, ACB, BCA, BAC, CAB et CBA représentent un seul choix) ou, au contraire différencier des choix ne différant que par l'ordre.

On a donc 2 cas : avec ou sans répétition et 2 cas : avec ou sans ordre. Commençons donc à faire des dénombrements : ça nous donne...4 cas à examiner.

Pourquoi 4 ? parce qu'il y a 2 cas pour la répétition et 2 cas pour l'ordre et qu'à chacun des cas pour la répétition correpondent les 2 cas pour l'ordre, ce qui donne : 2 x 2 = 4 !

On peut voir ça comme un tableau : 

AVEC ORDRE SANS ORDRE
AVEC REPETITION Cas1 Cas 4
SANS REPETITION Cas2 Cas 3

Donc, revenons à notre problème de départ que nous allons examiner dans chacun des 4 cas : combien y a-t-il de façons de choisir 3 lettres parmi A,B,C,D,E ?

 

Cas 1 : avec ordre et avec répétition
Ca veut dire que ABC et CBA ne sont pas pareils et qu'on peut avoir AAB.

Il y a 5 lettres possibles quand on doit choisir la première lettre : A, B, C, D ou E.
Une fois cette première lettre choisie, il y a toujours 5 possiblités de choix pour la deuxième, puisqu'on peut choisir la même (répétition autorisée).
Il y aura enfin, encore 5 possibilités de choix pour la troisième lettre (pour la même raison que précédemment).

A chacun des choix possibles pour la première lettre, correpondent tous les choix de la seconde :
Que la première soit A ou B ou C ou D ou E, la seconde peut être A ou B ou C ou D ou E; ça donne donc 25 (5x5) façons de choisir les deux premières lettres :
AA AB AC AD AE BA BB BC BD BE CA CB CC CD CE DA DB DC DD DE EA EB EC ED EE

Et ce sera pareil pour la dernière : 5 choix possibles (ABCDE) pour chacun de 25 cas précédents, donc au total 5 x25 = 125 choix possibles !

Remarque : 125 a été obtenu en multipliant 5 par 5 puis encore par 5, soit 5x5x5, soit 53

Si on généralise le problème, non plus à 3 lettres à choisir parmi 5, mais à p objets à choisir parmi n, par un raisonnement analogue, la réponse sera donc : n multiplié par n, puis par n, puis par n...(p fois), donc :  np

Le nombre de façons de choisir p objets parmi n avec ordre et avec répétition vaut :   np

 



Cas 2 : avec ordre mais sans répétition
Quand la première lettre choisie est un A, la seconde ne peut plus être un A (puisque la répétition n'est pas autorisée), ça sera donc un B, un C, un D ou un E (4 possibilités de choix, 4 = 5 - 1, 5 possibilités au départ moins 1 puisqu'on ne peut pas choisir la même lettre une seconde fois). Il n'y aura ainsi plus que 3 possibilités de choix pour la troisième lettre qui ne pourra être aucune des deux premières.

Comme tout à l'heure, à chaque choix de la première lettre, correspondent tous les choix de la seconde, ce qui nous donne 20 façons de choisir les deux premières (20 = 5x4) :
AB AC AD AE    BA BC BD BE    CA CB CD CE    DA DB DC DE    EA EB EC ED

Pour chacune de ces 20 configurations, on aura 3 possiblités de choix pour la troisième lettre, donc 20x3 = 60 = 5x4x3 façons de choisir 3 lettres parmi 5 avec ordre mais sans répétition.

Si on généralise le problème, non plus à 3 lettres à choisir parmi 5, mais à p objets à choisir parmi n, par un raisonnement analogue, la réponse sera donc : n multiplié par n-1, puis par n-2,.... puis par n-p+1 (p termes), donc :

 nx(n-1)x(n-2)x(n-3)...x(n-p+1)


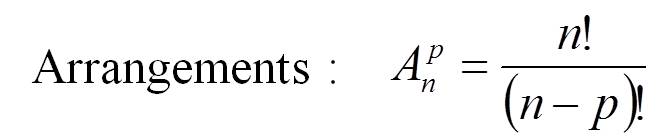
Exemple : Combien y a-t-il de façons de choisir 6 lettres dans l'alphabet avec ordre mais sans répétition :

26 x 25 x 24 x 23 x 22 x 21 (6 termes décroissant à partir de 26)

Cas 3 : sans ordre et sans répétition


Pour résoudre ce cas-là, revenons au résultat obtenu dans le cas précédent : il y avait 60 façons de choisir 3 lettres parmi 5 sans répétition mais avec ordre :

ABC BAC CAB DAB EAB
ABD BAD CAD DAC EAC
ABE BAE CAE DAE EAD
ACB BCA CBA DBA EBA
ACD BCD CBD DBC EBC
ACE BCE CBE DBE EBD
ADB BDA CDA DCA ECA
ADC BDC CDB DCB ECB
ADE BDE CDE DCE ECD
AEB BEA CEA DEA EDA
AEC BEC CEB DEB EDB
AED BED CED DEC EDC

Quand l'ordre comptait, il y avait 60 façons de choisir; que se passe-t-il quand l'ordre ne compte plus : si on regarde dans le tableau, on s'aperçoit que, par exemple, il y a 6 cas correpondant au choix de A,B et C (ceci est vrai pout n'importe quelle combinaison de 3 lettres).
Si 2 choix qui ne diffèrent que par l'ordre représentent un sul choix, il convient de compter ces 6 cas comme un seul et même cas, et de faire de même avec toutes les autres combinaisons de 3 lettres.
On se trouve donc avec des combinaisons de 3 lettres toutes comptées 6 fois au lieu d'une seule.
Pour répondre à la question, il faut donc prendre le résultat précédent : 60 et le diviser par 6 !

Il y a donc 60/6 = 10 façons de choisir 3 lettres parmi 5 sans ordre et sans répétition

 

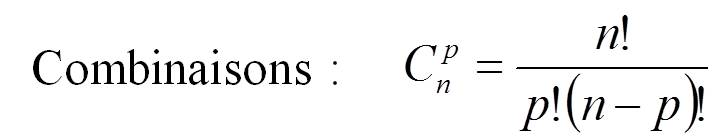
Cas 4 : sans ordre et avec répétition

Pour résoudre ce cas, qui est de loin le plus difficile et qui est, de ce fait, rarement évoqué, il faut complètement changer de point de vue :

Dans ce cas, la seule chose qui compte est de savoir combien on choisit de A, de B, de C, de D, de E (0 choix possible) sachant que le total de choix est de 3.

Imaginez 5 boites : ABCDE et 3 jetons, cela revient donc à dénombrer le nombre de façons de mettre les 3 jetons dans les 5 boites.

Ainsi : ooIIIIo (les "o" pour les jetons et les "I" pour les séparations entre les boites)

représenterait 2 jetons dans la première boite (A), pas de jeton dans le 3 boites suivantes BCD et 1 jeton dans E

soit AAE

Comme l'indique la représentation, il faut donc ranger 3 jetons (cas général : p) et 4 "cloisons" (cas général : n-1) sur 7 places disponibles (cas général : n+p-1)

En remarquant que si l'on choisit la place des p jetons, les n-1 cloisons seront automatiquement placées, le nombre de choix est :



RETOUR A L'ACCUEIL