LA LOI BINOMIALE

 

 

La loi binômiale se définira de la manière suivante :

 

Considérons une succession d'épreuves identiques et indépendantes,

 

chaque épreuve pouvant se solder soit par un succès, soit par un échec.

 

Si l'on note p la probabilité de succès à une épreuve

 

et si l'on définit la variable aléatoire X comme étant le nombre de succès obtenus en n épreuves,

 

on dira (par définition) que X suit une loi binômiale de paramètres n et p

 

On note :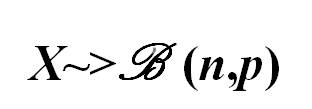       

 

(le premier paramètre n représente le nombre d'épreuves, le second p représente la probabilité de succès à une épreuve)

 

Exemple : Si l'on note X le nombre de "6" obtenu en lançant 12 dés, on sait que X suivra une loi binômiale de paramètres 12 et 1/6.

 

Nous allons maintenant déterminer la distribution de probabilité d'une loi binômiale, c'est à dire la probabilité qu'elle prenne telle ou telle valeur.

 

Remarquons tout d'abord que le nombre de succès en n épreuves peut aller de 0 à ... n.

 

Nous allons donc déterminer P( X = k ) pour k prenant toutes les valeurs entre 0 et n

 

Avoir k succès en n épreuves, c'est aussi avoir n-k échecs.

 

La probabilité d'avoir un succès est notée p; la probabilité d'avoir un échec sera notée q et vaudra bien sûr 1-p.

 

La probabilité d'avoir k succès puis n-k échecs lors d'une succession de n épreuves vaudra donc :

 

 

Mais cette probabilité ne représente qu'un des cas où les n épreuves comportent k succès : c'est celui où tous les succès ont lieu d'abord.

 

On peut imaginer quantité d'autres cas, par exemple, tous les succès peuvent avoir lieu à la fin, ou au milieu, ou après 3 épreuves, ou en alternance avec les échecs, etc...

 

De toutes façons, chacun de ces cas aura la même probabilité d'apparition que le premier évoqué, c'est à dire pk qn-k

 

Pour déterminer la probabilité d'avoir k succès (X=k), il suffit donc de compter tous ces cas.

 

Or il y a autant de cas que de façons de choisir la place des k succès parmi les n épreuves (la place des échecs est toute désignée une fois choisie celle des succès), il y en a donc : .

 

La probabilité cherchée vaut donc :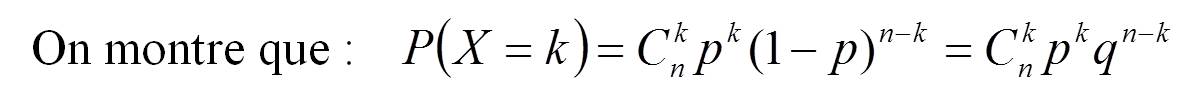

 

 

Exemple : Si l'on veut appliquer la formule pour déterminer la probabilité qu'il y ait 3 faces "6" lors du lancer de 12 dés, cela donne : 0,1615.

 

 

Nous allons maintenant donner l'Espérance et la Variance d'une loi binômiale (sans calculs) :

 

E(X) = np

 

V(X) = npq

 

 

Ce qui donne, toujours dans l'exemple considéré, une espérance de 2 et une variance de 5/3.


LA LOI HYPERGEOMETRIQUE
 

 

 Considérons une population de N individus partagée en deux : les individus "positifs" en proportion p (donc au nombre de Np) et les individus "négatifs" en proportion 1-p notée q (donc au nombre de Nq)
 

Supposons qu'on prélève dans cette population un échantillon aléatoire de n personnes, cet échantillon étant prélevé sans remise.
 

Si on s'intéresse au nombre de personnes positives dans cet échantillon, on dira, par définition, qu'il suit une loi hypergéométrique de paramètres N,n,p

.

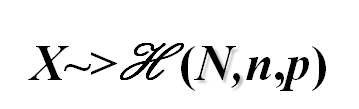  Notez qu'il y 3 paramètres pour une loi hypergéométrique : le premier, c'est la taille de la population; le deuxième, c'est la taille de l'échantillon; le troisième, c'est la proportion initiale d'individus positifs dans la population (initiale car cette proportion est constamment modifiée puisque le tirage est effectué sans remise).

   

Notez aussi qu'on pourrait parfaitement définir la loi binômiale comme on vient de définir la loi hypergéométrique; la seule différence est qu'alors le tirage devrait être effectué avec remise, les individus de l'échantillon représentant des épreuves et les individus positifs, des succès.

 

Cette remarque sera utile dans la suite, hypergéométrique : sans remise et binômiale : avec remise.

 

Cela dit, si n est "petit" par rapport à N (dès que le rapport n/N, appelé taux de sondage, est inférieur à 1/10) on pourra assimiler la loi hypergéométrique à la loi binômiale.

 

 

La distribution de la loi hypergéométrique est la suivante :

 

En effet, le nombre d'échantillons possibles est égal à  et le nombre de cas favorables s'obtient en multipliant le nombre de façons de choisir les k individus positifs (parmi Np) et les n-k individus négatifs (parmi Nq)

 

L'espérance est égale à :                    n p                                     (comme la loi binômiale).

 

La variance vaut :                     

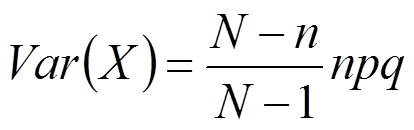
( s'appelle facteur d'exhaustivité).

 

 

 

Remarque : Ce facteur étant clairement plus petit que 1, on en déduit que la variance de la loi hypergéométrique est inférieure à celle de la loi binomiale associée.

 

Donc que la variance du nombre d’individus positifs dans un échantillon est plus faible si l’échantillon est prélevé sans remise qu’avec.